GM Jackson Physics and Mathematics How to Derive the Laplace Operator "Laplacian" for Spherical
Solution of Laplaces Equation in Spherical coordinates by

The 2D Laplacian operator is presented for the Cartesian and polar coordinates, and in the 3D case for the extended Cartesian, polar, and spherical coordinates. The BCs include Dirichlet, Neumann, and mixed or "Robin" equations for a function, its derivative, and their linear combination, respectively.
GM Jackson Physics and Mathematics How to Derive the Laplace Operator "Laplacian" for Spherical

Note. Equation (6.5.6) is a key equation which occurs when studying problems possessing spherical symmetry. It is an eigenvalue problem for Y(θ, ϕ) = Θ(θ)Φ(ϕ), LY = − λY, where L = 1 sinθ ∂ ∂θ(sinθ ∂ ∂θ) + 1 sin2θ ∂2 ∂ϕ2. The eigenfunctions of this operator are referred to as spherical harmonics.
Laplacian in spherical coordinates derivation part 1 YouTube

Let \(\Delta \) denote the Laplace-Beltrami operator on X and let \(\rho \). It is a feature of these coordinates that the tangent space at the center is isometric to the standard n. Integral geometry, invariant differential operators, and spherical functions. Mathematical Surveys and Monographs, vol. 83. American Mathematical Society.
Laplacian in spherical coordinates Part3 (final) YouTube

Laplace operator in spherical coordinates; Special knowledge: Generalization; Secret knowledge: elliptical and parabolic coordinates; 6.3. Laplace operator in polar coordinates. In the next several lectures we are going to consider Laplace equation in the disk and similar domains and separate variables there but for this purpose we need to.
Mathematics Free FullText Do It by Yourself An Instructional Derivation of the Laplacian

To solve Laplace's equation in spherical coordinates, attempt separation of variables by writing. (2) Then the Helmholtz differential equation becomes. (3) Now divide by , (4) (5) The solution to the second part of ( 5) must be sinusoidal, so the differential equation is. (6)
SOLUTION Step by step derivation of 3D Laplacian in terms of spherical polar coordinates

3.5.2 Spherical coordinates In Sec. 3.4.4 we presented the form on the Laplacian operator, and its normal modes, in a system with circular symmetry. In addition to the radial coordinate r, a point is now indicated by two angles θ and φ, as indicated in the figure below. The original Cartesian coordinates are now related to the spherical.
Solution of Laplaces Equation in Spherical coordinates by

Laplace operator in spherical coordinates; Special knowledge: Generalization; Secret knowledge: elliptical coordinates; Laplace operator in polar coordinates. In the next several lectures we are going to consider Laplace equation in the disk and similar domains and separate variables there but for this purpose we need to express Laplace.
Solved Show that the Laplace operator in spherical

where r is the radial part containing derivatives with respect to ronly, and s is the spherical part containing derivatives with respect to the angular coordinates. For future use, it is convenient to consider a more general equation of the form L ru+ 1 r2 su= 0; (1) where L r is any operator involving only derivatives with respect to r. Our rst task is to separate the variables, and deal with.
GM Jackson Physics and Mathematics How to Derive the Laplace Operator "Laplacian" for Spherical

In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space.It is usually denoted by the symbols , (where is the nabla operator), or .In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable.
GM Jackson Physics and Mathematics How to Derive the Laplace Operator "Laplacian" for Spherical

2. Write the potential on the surface in terms of Legendre polynomials. This step is crucial in comparing coefficients, and we can use trigonometric identities to do this. We then refer to the zeroth, second, and fourth polynomials to write in terms of them. 3. Solve for the potential outside the sphere.
L17.1 Laplace equation in spherical polar coordinates YouTube

Laplace operator in spherical coordinates; Special knowledge: Generalization; Secret knowledge: elliptical coordinates; Laplace operator in polar coordinates. In the next several lectures we are going to consider Laplace equation in the disk and similar domains and separate variables there but for this purpose we need to express Laplace.
[Solved] Laplacian of spherical coordinates 9to5Science
The basic idea is to take the Cartesian equivalent of the quantity in question and to substitute into that formula using the appropriate coordinate transformation. As an example, we will derive the formula for the gradient in spherical coordinates. Goal: Show that the gradient of a real-valued function \(F(ρ,θ,φ)\) in spherical coordinates is:
GM Jackson Physics and Mathematics How to Derive the Laplace Operator "Laplacian" for Spherical
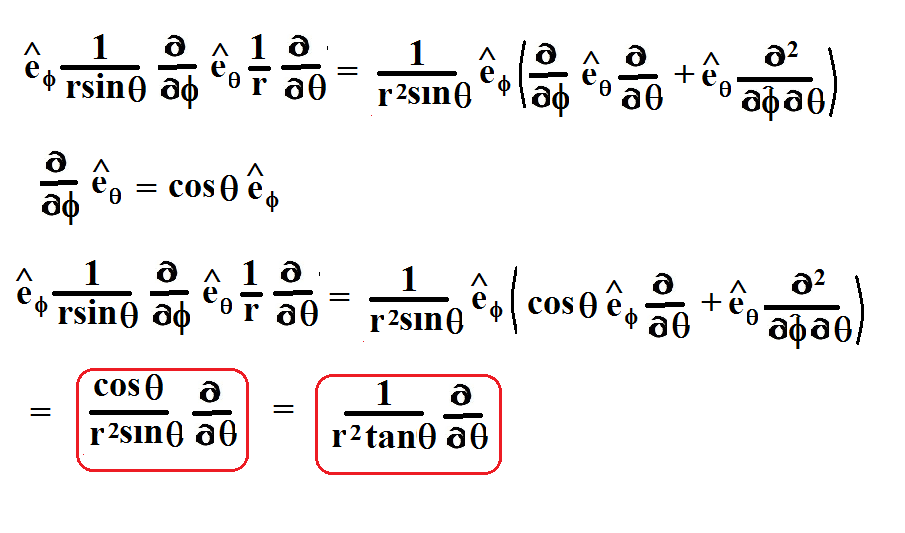
The Laplacian operator in the cylindrical and spherical coordinate systems is given in Appendix B2. This page titled 4.10: The Laplacian Operator is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Steven W. Ellingson (Virginia Tech Libraries' Open Education Initiative) .
Laplace Operator in Spherical Coordinate of R^n.pdf Google Drive
And finally the Laplacian operator is $$\nabla^2=\frac{1}{r^2\sin(\phi)}\left(\frac{\partial}{\partial r}\left(r^2\sin(\phi)\frac{\partial}{\partial r. I recently went through the computations to convert the Laplacian to spherical coordinates and was lucky to find a slick method in C.H. Edwards' Advanced Calculus of Several Variables.
SOLUTION Laplace equation in spherical coordinates Studypool

The Laplacian Operator in Spherical Coordinates Our goal is to study Laplace's equation in spherical coordinates in space. Here we will use the Laplacian operator in spherical coordinates, namely u= u ˆˆ+ 2 ˆ u ˆ+ 1 ˆ2 h u ˚˚+ cot(˚)u ˚+ csc2(˚)u i (1) Recall that the transformation equations relating Cartesian coordinates (x;y;z.
partial derivative Laplacian operator in spherical coordinates (two particles) Mathematics

1Laplace's Equation in Spherical Coordinates: The General Case REMARK: In this pdf I expand the 3 page discussion (pp. 220 - 222) to 7 pages in order to clarify a number points the textbook author does not provide. As discussed in the textbook, Laplace's equation in spherical coordinates for the function u(ˆ; ;˚) takes the form u ˆˆ+ 2.